Free fall – Modeling using Matlab

In this post, we will simulate the fall of an object dropped from a certain height in air. We will be using some numerical technique to find the time at which the speed of the object stop changing and to find out if this speed is reached before the object reach the ground.

We will  be using Matlab and the Euler method to model the free fall of this object.

First we need to find mathematical equations for the given problem. We are going to use Newton’s equation of motion in 1d and will be taking into account the gravity force and the air friction opposing to the falling of the object.

Mathematically thinking, we have equation below, the equation (1) is the equation overall assumed force acting of the free falling object where m is the weight and a is the acceleration of the free falling object.

(2) is the the total force expressed in term of the gravitational force and the air friction acting of the object.

In (3) we can take g (standard acceleration due to free fall) to be 9.80665 m/s²

At a certain point the velocity of the free falling object stops changing thus making the acceleration to be zero. The equation (6) shows what that velocity is which in our case is the final velocity of the object.

The following equation is the equation using for numerical method to help us find the first derivative of a function without having  to find the derivative itself.

We will be using the Euler method to solve the first order differential equation obtained above in (5)

Have in mind that (5) can also be written like the following

Since the acceleration is the derivative of the velocity over time.

Now plugging the last equation into the Euler equation we have the following equation.

We will consider values below to simulate this exercise. Remember that to use this method we need initial conditions, and remember at the time t=0 the velocity v=0.

Coding this in Matlab will look like this.

clear all;
V0=0; % initial speed
m=5; % mass in kg
g=9.81; % gravity acceleration kg/m3
rho=1.2; % Air density
A=0.09; % Object area
cw=0.4; % Numerical drag coefficient
k=0.5*cw*rho*A; % Coefficient
N=100; % Time step
V=zeros(1,N); % Speed
V(1)=V0;
deltat=0.2;
for i=1:N-1
V(i+1)=V(i)+deltat*(g-(k/m)*V(i)^2);
end
t=(0:N-1)*deltat;
vterminal=sqrt(g*m/k); % Terminal velocity
plot(t,V,t,ones(1,N)*vterminal);
xlabel('time in sec');
ylabel('velocity in m/s');
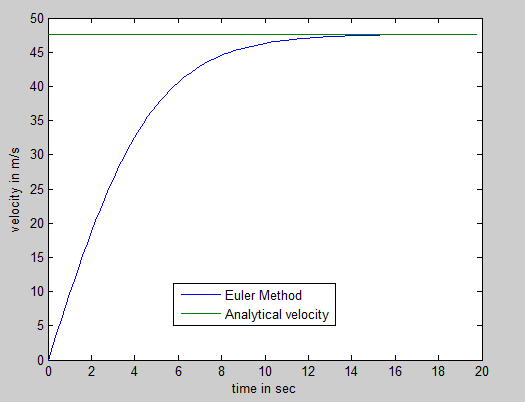
legend ('Euler Method', 'Analytical velocity','location','south');

If you copy the code above and paste it into the Matlab software you will have the following image explaining what is happening to the object when it is free falling. velocity increases until a certain value and remains constant.

You can twist the code to find out how long the object takes to reach the floor and much more.