Here is a comparison between the Implicit Euler Method and the Explicit Euler method on a given RLC circuit.
We will be using the two methods stated above to model the variation of the current in the circuitry below.
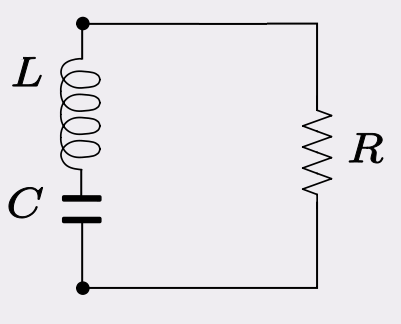
RLC simulation in Matlab
We consider the capacitor voltage to be zero at the zero time.
From the equation of the current in an inductance, the voltage in a capacitor and solving KVL (kirchhoff’s voltage law) in the loop we will have the following equation. (KVL = Voltage in the capacitor + voltage in the inductance + Voltage in the Resistor = zero)
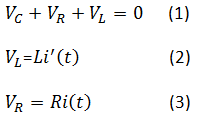
With (2) and (3)
(1) becomes
Then rearranging it to have the derivative on one side
Looking now at what the voltage will be in the capacitor over time.
So, the following couple of equation are the ones that we will be using in the remaining part.
Explicit Euler Method
Putting our equation in this form, we will end up with
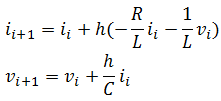
Implicit Euler Method
Putting our equation in this form, we will end up with
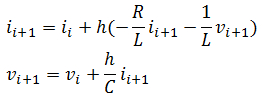
We need to solve this system of equation such as having them look like this
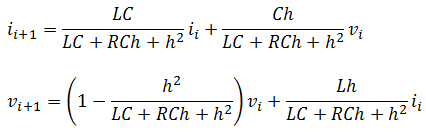
Let’s now write a code giving these information to Matlab to investigate how the current in this loop changes over time.
clear all;
close all;
i0=1; % current at t=0
v0=1; % Capacitor voltage at t=0
L=1.5; % Inductance value in Henry
C=0.0001; % capacitance in F
R=0; % resistance in Ohm, R is considered to be zero
h=0.001; % time interval
N=500; % number of iteration
i=zeros(1,N);
v=zeros(1,N);
t=zeros(1,N);
i(1)=i0;
v(1)=v0;
t(1)=0;
i2(1)=i0;
v2(1)=v0;
for n=1:N
t(n+1)=n*h; % Explicit Euler Method
i(n+1)=i(n)+(-R/L*i(n)-1/L*v(n))*h;
v(n+1)=v(n)+1/C*i(n)*h; % Implicit Euler Method
i2(n+1)=L*C/(L*C+R*C*h+h^2)*i2(n)-C*h/(L*C+R*C*h+h^2)*v2(n);
v2(n+1)=(L*C+R*C*h)/(L*C+R*C*h+h^2)*v2(n)+L*h/(L*C+R*C*h+h^2)*i2(n);
end
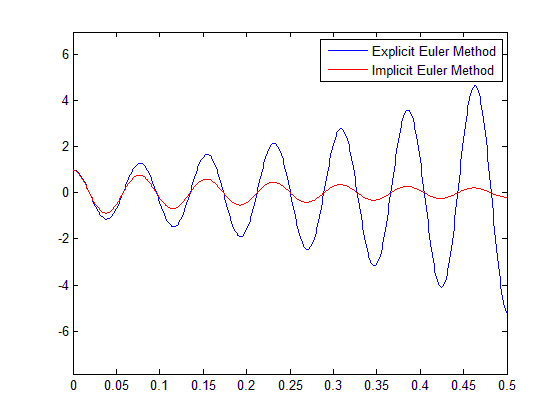
plot(t,i,t,i2)
axis([0 h*N 1.5*min(i) 1.5*max(i)])
legend('Explicit Euler Method', 'Implicit Euler Method')If you write this exact code in Matlab you will see the image below popping up as a result of this experiement.
All values are given in the code for you to easily understand and replicate this experiment.
Feel free to drop a comment below.
Leave a Reply